RAM Compression Analysis But first, a word from our sponsor, O'Reilly & Associates...
A monthly survey of online-publishing standardization and specifictions

RAM Compression Analysis

Mark Russinovich and Bryce Cogswell

February 1, 1996

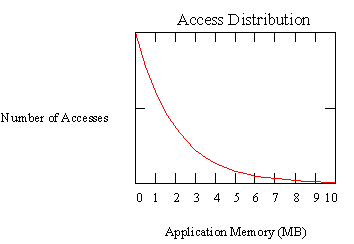
This document presents a mathematical model that we have derived for the technique of providing a system with a compressed pagefile ("swap file") cache. The fundamental concept that makes the model possible is viewing the code and data space of an application as a set of memory pages, each of which is accessed with varying frequency. Typically, applications exhibit roughly an exponential access distribution, meaning that if a graph is drawn with pages ordered with respect to the number of times they are accessed on the x-axis, and the number of accesses on the y-axis, that the distribution will look something like this:

Because Windows uses a Least Recently Used aging scheme for selecting pages to swap to disk, the exponential distribution above will match closely the page faulting behavior of the application. This means that if a vertical line is drawn through the graph at x=2, which would represent only 2MB available physical memory, that the sum of all the accesses to the right of that line (which is the integral under the exponential curve to the right of the line) will equal the number of page faults incurred by the application since these are accesses to pages that do not fit into memory.

By measuring the number of page reads and writes that occur during an application's execution, the curve representing the integral referred to above can be obtained. It in fact, will also have an exponential curve to it. Thus, using the following graph of number of page faults given a certain memory size, one can determine the number of page faults on a machine of 8MB by looking at the value of the curve at that point.

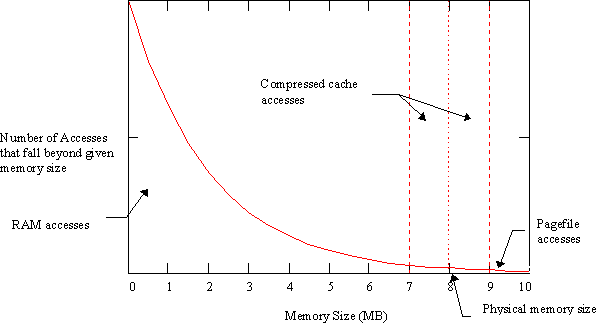
All accesses to the right of the physical memory line result in page file accesses (disk accesses), while those to the left of the line are accesses to pages that are in physical RAM.

A compressed paging cache has several effects on the system. The first is that the system's usable memory size will decrease (line moves to the left) an amount equal to the size of the compression buffer. For example, if 1MB was taken for the compressed pagefile cache, Windows would only have 7MB to use for application memory, and the application would therefore generate page faults as if it were running on a 7MB machine. This is the first factor in determining cache effectiveness: causing more page faults.

The second effect of the pagefile cache is to create an intermediate range in the graph that extends on the x-axis from the place where the cache starts to the memory size and then beyond to a place determined by the compression ratio achieved. For example, if the cache was 1MB in size and a compression ratio of 2:1 is obtained, the cache effect area would extend from 7MB to 9MB (8MB memory size -1MB cache size + 1MB cache size * compression ratio of 2). This is shown in the graph below:

Because all page faults pass through the cache before making it to disk, any accesses to the right of the line at 7MB are accesses subjected to compression (and possibly decompression). This is the second factor in determining cache effectiveness: overhead of compression.Access that are to the right of the physical memory size line and to the left of the right cache line (at 9MB above) represent accesses that without the cache in place would have been disk accesses. With the cache in place, these accesses actually fall in the cache. This is the third factor in determining cache effectiveness: the number of disk accesses saved.

It should now be clear that for a cache to be effective, it basically has to satisfy the following releationship:

Overhead of compression for all accesses to the right of the buffer start (7MB in the example) must be less than the amount of time saved in avoiding disk I/O.

An additional factor that impacts a real implementation of pagefile caching under Windows 95 that is not taken into account in the above model is disk cache misses caused because the disk cache sizing policy is not set up to understand the effects of a pagefile cache. Another factor is additional disk accesses caused because the compression management strategy will most likely occasionally break page file writes, that come in blocks of 8 pages, into multiple writes in order to fit compressed pages into spots in the page file.

In order to get an idea of how well pagefile cacheing would work for real Windows applications, we measured the pagefile read and write rates of the Ziff-Davis Winstone benchmark. This gives us the access curves described above. The next thing we did is implement a pagefile cache compressor so that we could measure compression/decompression versus disk access overheads as well as compression ratios on the actual Winstone paging data.

We then derived a mathematical expression for the model described above and plugged in numbers obtained from the measurements. The result we obtained was that although it appears possible in theory to obtain a benifit from a compressed pagefile cache, that for realistic parameters it is extremely difficult. The empirical evidence that backs this claim up are the performance of RAM Doubler, MagnaRAM 2, and our own implementation, all of which ended up lowering the Winstone score by significant amounts when a 1MB cache was used on an 8MB machine (incidentally, our implementation did the best by a wide margin, but still slowed the machine down).

Here are the parameters used in the model:

cd = time in seconds for compression or decompression operation
ch = time in seconds for hard disk read or write operation
r = compression ratio (actual size divided by compressed size)
m = physical memory available on machine (MB)
d = size of compressed cache (MB)
frac = number of additional disk accesses caused by compressed cache management for every pagefile write

The model takes into account both memory read accesses and memory write accesses. Essentially, all accesses that are to the right of the left side of the cache region in the graph cause an overhead of compression/decompression and whereas access to the cache region that are to the right of the physical memory size result in saved disk accesses. Therefore, each sub-equation takes the compression overhead and subtracts the saved disk accesses to obtain a total effect on performance i.e.:

performance effect = overhead of compression - time saved by avoided disk accesses

Positive results indicate a performance degredation (time added to a application's execution) and negative results are a performance improvement (time subtracted from an application's execution). The write execution equation has the additional term of overhead caused by increased pagefile writes (if any). The sum of the two sub-expressions (exec) is the overall effect of a compressed pagefile cache. The Read() and Write() functions used in the sub-expressions return the number of memory accesses that fall beyond the memory boundary passed as a parameter. For example, Read(8) returns the page faults, as determined through modeling or actual measurements, that occur when the application is run on an 8MB machine.

The rest of the document is broken down as follows: first the raw and interpolated data for Winstone pagefile reads and writes at varying memory sizes is shown. Then we present the values for the terms obtained from measurements and plug them into the model.

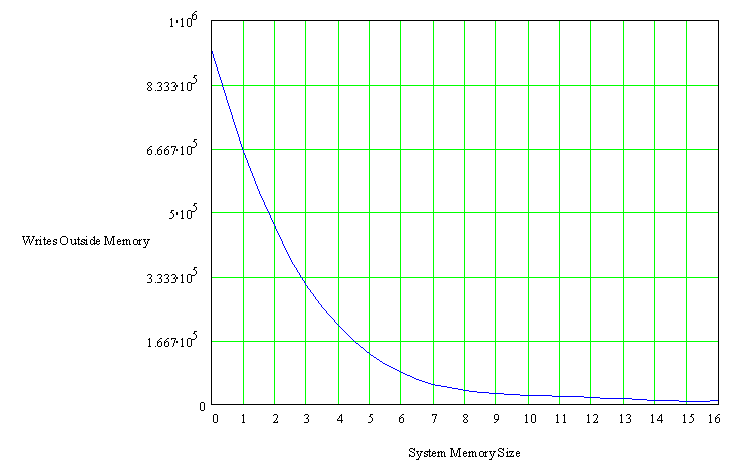
The following table shows the number of pagefile reads that occur for Winstone running with varying amounts of available memory (6MB, 7MB, etc.). Following the raw data is a graph of the data.

Memory (MB)	Pagefile Reads
6	229089
7	97257
8	55594
9	37678
10	26633
11	19379
12	14815
13	11193
14	8297
15	7065
16	5044

The graph below is an interpolated curve of the raw pagefile read data shown in the table.

Here is the raw data for Winstone's pagefile writes at varying memory sizes.

Memory (MB)	Pagefile Write
6	84533
7	51069
8	37106
9	30592
10	24964
11	20732
12	17599
13	14533
14	11700
15	10454
16	8479

Below is the interpolated curve for the pagefile write data.

Here we present the parameter values that we've determined through measurements.

cd = 2 milliseconds to compress or decompress a page
ch = 0.01 Disk access is about 10ms
r = 1.6 Copression ratio obtained for our algorithm on Winstone data
m = 8 Memory size of machine being modeled (MB)
frac = 0 Estimate at additional disk writes caused by cache management
d = [0..16] Size of compressed buffer (MB)

What we discovered in our measurements is that even though it only takes about 50 microseconds to compress a page with our compression algorithm, a page fault results in a significantly larger overhead. Thus, the compression time listed above incorporates the cost of Windows servicing a page fault. Given the parameters listed above, the curve below shows the overhead of a compressed pagefile cache versus the cache size. The least overhead occurs at a compressed pagefile cache size of about 0.8MB and is close to 100 seconds (1 1/2 minutes). In actual practice, our RAM compressor running with a 1MB cache lowered the Winstone score about 10% (higher scores are better), which is consistent with the benchmark taking the extra time indicated by the model. The dashed lines show the effects of the read and write sub-expressions.

What we have learned from this model and the measurements we have taken is that:

For realistic parameters RAM compression doesn't pay on the industry standard Winstone benchmarks
Even with high compression ratios and low compression overheads, improvements are small

Any questions or comments regarding this model are welcome. We can be reached at mer@cs.uoregon.edu and cogswell@cs.uoregon.edu.

Visit these other O'Reilly online areas:

Our homepage, with product information, feature articles, and more.

WebSite Central, home of O'Reilly's hot, new, Windows Web server.

The O'Reilly Windows Center has Win 95 programming information, articles, and links. FTP site, with newer versions.